ICS 312 Spring 2025

Homework Assignment #6 [55 pts]

You are expected to do your own work on all homework assignments. You may (and are encouraged to) engage in general discussions with your classmates regarding the assignments, but specific details of a solution, including the solution itself, must always be your own work. (See the statement of Academic Dishonesty on the Syllabus.

How to turn in?

Assignments need to be turned in via Laulima. Check the Syllabus for the late assignment policy for the course.

What to turn in?

You must turn in a zip archive named ics312_hw6_xxx.zip, where “xxx” is your UH user name (e.g., for me, it would be ics312_hw6_henric.zip). The archive must contain a single top-level directory called ics312_hw6_xxx, where “xxx” is your UH user name (e.g., for me, it would be ics312_hw6_henric). In that directory you must have all the files named exactly as specified in the questions below.

Expected contents of the ics312_hw6_xxx directory:

Deviation from the above specs will lead to lost points:

Overview

These exercises below all deal with displaying, as ASCII art in the terminal, a binary (i.e., black and white) bitmap image. The image is provided to you as a sequence of 32-bit integers. The first two integers are the height (h) and width (w) of the image, followed by a sequence of h×w integers, each of which encodes 32 pixels of the image. The pixels are encoded in a row-major fashion. That is, the first integer in the sequence encodes the first 32 pixels of the first row of the image. We assume that w is always a multiple of 32.

For instance, consider the following bitmap image (height 5, width=32):


The integer encoding of this image would be as follows (hex representation of pixel integers shown as comments):

5
32
1
1073741812
-1208016950
-469762050
2012151264

Exercise #1: Displaying an ASCII image [15 pts]

Implement a program called imagedisplay (source code in imagedisplay.asm) that reads in the following:

Given this input, the program should print the image as ASCII art: a 0-bit is printed as two white spaces (‘ ‘) and a 1-bit is printed as two hashpounds (‘##’). You can test your program by entering integers by hand (for instance for the sample image above), but for a large image that would be a lot of manual input. Instead, it’s better to have the sequence of numbers in a file, for instance example_image.numbers, with one integer per line. Say the content of that file is:

5
32
1
1073741812
-1208016950
-469762050
2012151264

then, invoking your program as:

cat example_image.numbers | ./imagedisplay

should produce this 5-line output:

                                                              ##
    ####################################################  ##    
##  ####  ######################      ##############    ##  ##  
######      ##################################################  
  ######  ############  ######  ############  ########

Here are several examples for you to test your code:

Bitmap image Size Input integers Expected output
100x128 bunny.numbers bunny.ascii
114x64 violin.numbers violin.ascii
386x480 turtle.numbers turtle.ascii
186x320 dragon.numbers dragon.ascii


For reference, my solution is 65 lines of code.

Exercise #2: Descrambling an ASCII image [25 pts]

It turns out that sending messages written in binary bitmap images is a thing now, but people try to scramble the pixels so that merely displaying the pixels as in the previous question not longer prints the correct (or decipherable) image! Luckily, you have spies out there, who have discovered the scrambling scheme: for each 32-bit integer the high 16 bits are reversed (as in a list reversal), and the low 16 bits are inverted (i.e., every 0 becomes a 1 and every 1 becomes a 0). For instance, if the original 32-bit integer is:

1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0

then the scrambled bits are:

1 0 1 0 1 0 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1

Implement a program called imagedescramble (source code in imagedescramble.asm) that is similar to the imagedisplay program, but descrambles the input integers before printing the ASCII art.

Here are several examples for you to test your code (the displayed images below are the ASCII outputs if you just run imagedisplay on the scrambled input):

Bitmap image Size Input integers Expected output
100x128 scrambled_bunny.numbers bunny.ascii
386x480 scrambled_turtle.numbers turtle.ascii
53x128 scrambled_hidden_message.numbers Some legible sentence


For reference, my solution is 87 lines of code (i.e., 22 lines of code added to the program from Question #1).

Exercise #3: Decrypt an ASCII image [15 pts]

People out there discovered that you’ve been easily descrambling their scrambled images and messages, and have resorted to a more serious encryption scheme. Your team has been unable to figure it out until recently, when one of your operatives was able to get a hold of the C code that is used to encrypt each 32-bit integer. And, extremely stupidly, the encryption key is hardcoded in the code, which makes it possible to implement the inverse operation!

The C code, which interprets the original integer (original_integer variable) as an UNSIGNED value, is as follows:

unsigned int encryption_key = 1374123;
unsigned int encrypted_integer;
unsigned short us = (original_integer >> 20);
unsigned int tmp = (original_integer << 12);
tmp ^= (encryption_key * row * row);
tmp &= 0xFFFFF000;
encrypted_integer = tmp + (unsigned int) us;
encrypted_integer = (encrypted_integer << 29 ) | (encrypted_integer >> 3);

Implement a program called imagedecrypt (source code in imagedecrypt.asm) that is similar to the imagedisplay program, but decrypts the input integers before printing the ASCII art.

Here are several examples for you to test your code (the displayed images below are the ASCII outputs if you just run imagedisplay on the scrambled input):

Bitmap image Size Input integers Expected output
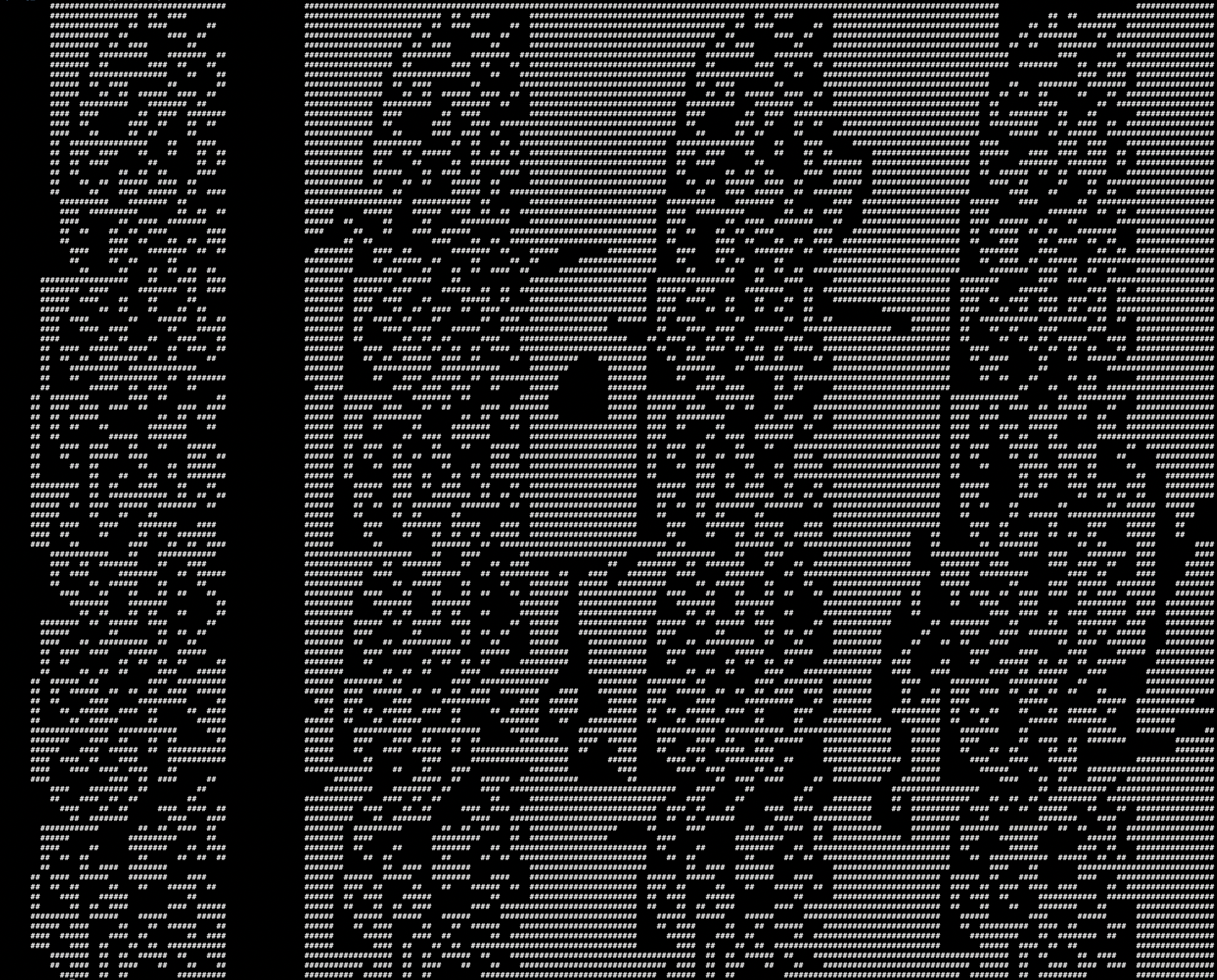
100x128 encrypted_bunny.numbers bunny.ascii
386x480 encrypted_dragon.numbers dragon.ascii
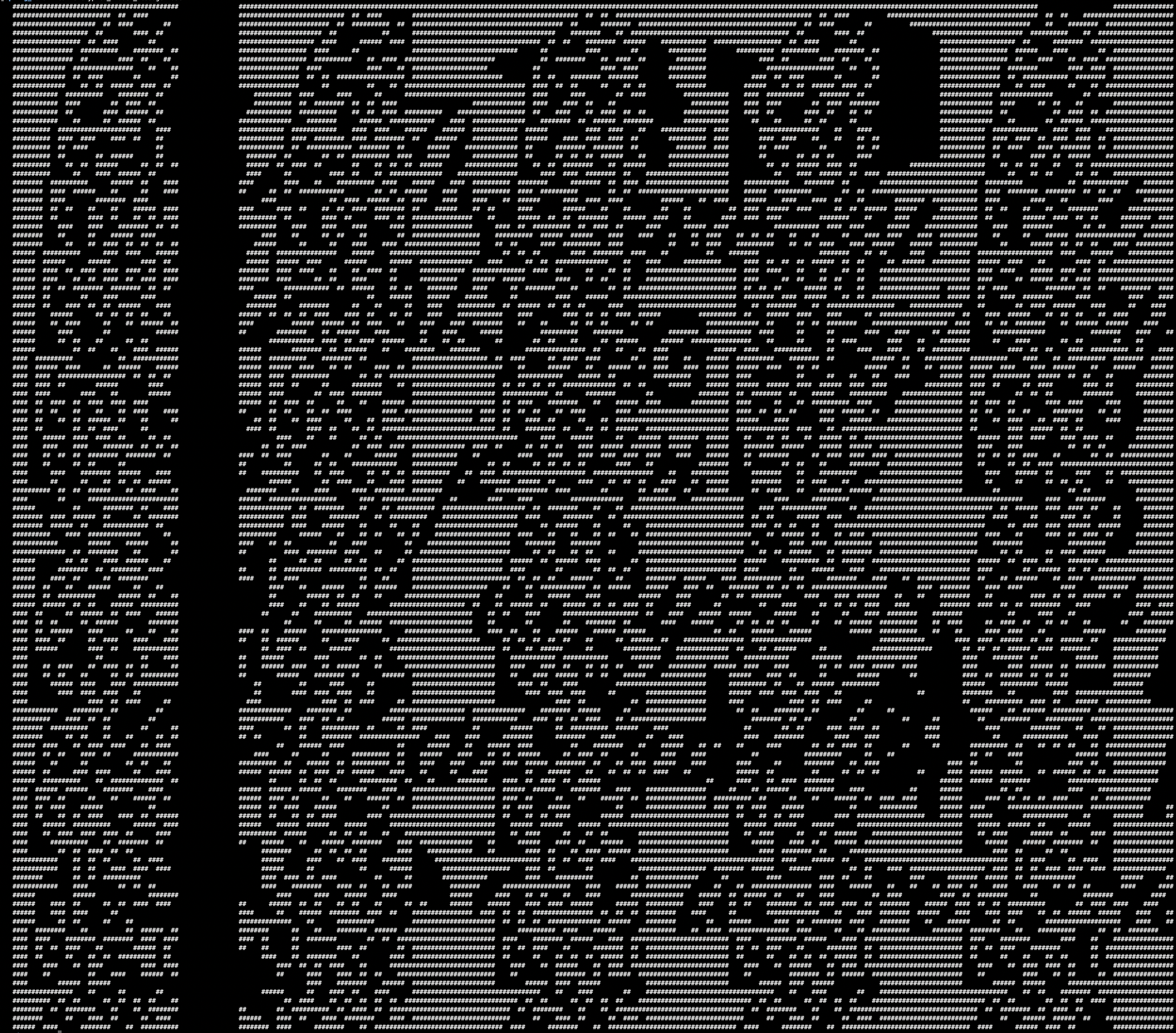
117x160 encrypted_hidden_message.numbers Some (other) legible sentence


For reference, my solution is 81 lines of code (i.e., 16 lines of code added to the program from Question #1).

Hints:

- A good approach is to trace what the C code does on a given 32-bit value, understand what it does, and then implement the reverse operation. This is much better than trying to reverse the process, say, line by line in the C code.  Doing this on an example binary string of 0's and 1's is likely the most eye-crossing endeavor ever. Instead, say that the input 32 bits are "abcdefghijklmnopqrstuvwxyzABCDEF" so that you can easily keep track of where bits move. 

- Remember that A ^ B ^ B = A

- Remember that in assembly we have more control about bits. That is, something that could be a few steps/operations in C are doable in a single instruction in assembly

- You'll have to do a multiplication. Make sure you use the correct multiplication instruction (given the signedness of numbers).